Output Decomposition Problem

Introduction

Some time ago professor Claudio Schifanella and I proposed a protocol acting like a decentralized mixer we called DMix (paper,demo,demo implementation). In this mixer, users interact to swap funds between each other. To maintain privacy, the output of the final transaction (the one from the mixer to the users) are all equal.

On the one hand, having many equal outputs in a transaction is the best (and easiest) way to increase privacy, since it maximize the number of possible IOmappings (i.e. the mapping between inputs and outputs of a transaction, see below for explicit definitions). On the other hand it has some practical drawbacks that prevent a smooth flow. It is important to note that the less friction the more the mixer is used, the higher the anonymity size, and therefore the higher the privacy. the principal drawbacks are:

• Higher fees: for each added amount, the cost of a transaction increases
• Input restriction: since all outputs have the same amount, the input must share a common divisor d (i.e. txInput_i = d ⋅ k_i for all i). We dealt with this problem by requiring parties to compute the Greatest Common Divisor on the inputs, which prevents them to submit any input and it is arguably a non-needed privacy leak in case of abort

Turns out that we share the same problem CoinJoins have. The problem is called Output Decomposition Problem and can be roughly stated as:

Output Decomposition Problem: for a given set of transaction input find the least number of outputs that maximize the possible IOmappings.

So this is what this post is about. We want to understand this Output Decomposition Problem by looking at the relevant literature and the proposed solutions. The end goal is to increase the privacy of DMix while making it more usable at the same time.

Insert table of contents

Problem Definitions

In the following we see some definitions related to the problem at hand.

• Knapsack problem: The knapsack problem is a combinatorial optimization problem in which a set of items with individual values and sizes are given, and the goal is to find the subset of items with the highest total value that can fit into a knapsack with a limited capacity. While this problem is NP-complete, various algorithms and heuristics have been developed to solve the knapsack problem efficiently for specific cases or with a certain level of approximation. You may see some resemblance between the knapsack problem and the output decomposition one: we have two measures and we want to minimize one and maximize the other at the same time.
• UTXO transaction: a UTXO (unspent transaction output) transaction is a type of transaction that represents the transfer of ownership of a specific amount of cryptocurrency from one user to another. It may be represented as a list T = (I|O) where I = (i₁, i₂, …, i_n) is the list of inputs and O = (o₁, o₂, …, o_m) is the list of outputs (note that in general n ≠ m.
• “Original” transaction: intuitively, this is a UTXO transaction T that has not been subjected to any transformation. In other words, T is the transaction the user would like to push to the blockchain if he/she did not care about privacy. We may refer to the inputs of this T as original inputs, and to the outputs as original outputs.
• Input-output transaction mapping (IOmapping): it is the link between the inputs and the outputs. In other words, this can be thought of which inputs funds which outputs in a transaction
• Possible IOmapping: some times the IOmapping is not unique and many possible mapping are formally true, without any external knowledge. See image below for a transaction with more than one possible IOmapping

The mapping spectrum:

It is easy to see that the less random the output are, the higher the number of possible IOmappings. Moreover, a higher number of IOmappings means higher privacy since many tracking heuristics will fail. See image below. Transactions T1 and T2 represent both a possible payment from Alice to Bob. Note that, assuming both transactions are in the blockchain, any adversary can see them as represented below

If I were an adversary, then:

• since there is only one possible IOmappings in T1, I know (i.e. I put a high probability) that it is a payment. I may not know where the input come from, But I can infer that the second output is the change address and the first one is the payment¹, especially if the address of the first output is public as it is often the case if Bob is a shop.
• I can not have the same degree of certainty if the same payment is done with T2. In this case Bob could use an address derivation system for commerce, like the one explained here, and produce two addresses. Or it may be a CoinJoin with multiple IOmappings. Or any other combination of the two.

It seems safe then to see the number of possible IOmappings as a proxy for privacy-measurement (but as mentioned IOmappings alone can not be a parameter since it can increase transaction fees and usability if done naively like original DMix):

Solutions

We can now try to find the solution. To do that we will look at the following papers:

• [Sax14]: Increasing Anonymity in Bitcoin(see PDF) by Saxena
• [Mau17]: anonymous coinjoin transactions with arbitrary values(see PDF) by Felix Konstantin Maurer, Till Neudecker and Martin Florian
• [Ni22]: mixing transactions with arbitrary values on blockchains(see PDF) by Wangze Ni, Peng Cheng and Lei Chen

Surprisingly, I could not find other papers dealing with the problem at hand directly. Of course many decentralized mixer proposals do acknowledge the problem, but their solutions are either naive or not treated at all. ²

[Sax14]

The authors introduce the idea of using the knapsack problem to increase the number of possible IOmappings, but no practical way to do that is presented

[Mau17]

The core idea presented in this paper is to modify “original” transactions to maximize the number of possible mapping. The authors propose three strategies:

1. dissect outputs
2. dissect inputs
3. dissect both

For easiness of explanation, we start from output dissection. The authors present an algorithm such that given two sets of inputs splits the biggest output in a way that leaves room for more IOmappings. Looking at the figure above it is easy to spot the general idea of the algorithm: the difference diff between the two sets is computed, and then the biggest output o is split into o₁ = o − diff and o₂ = o − o₁. this naturally leads to multiple IOmapping possibilities.

Then, the authors argue that output dissection has no effect on the inputs, so a shuffle of them is proposed. Of course the two kinds of dissection can be joined together into a full fledged algorithm.

In the latter part of the paper, the authors argue that this splitting method decrease traceability of CoinJoin transactions.

[Ni22] :

Differently from [Mau], the paper by Wan et al. focuses only on the outputs of the transactions.More clearly, instead of splitting outputs based on some difference between the inputs, [Ni22] focuses on a real re-decomposition of the outputs.

The authors present a multi-round protocol that, starting from the original outputs, creates new derived outputs. The number of rounds is decided beforehand: the higher the number of rounds (up to a threshold) the higher the number possible IOmappings. of course, the transaction broadcasted to the blockchain is the one with the derived output.

the algorithm can be summarized in this way. given n original outputs oo₁, ..., oo_n ordered from the highest amount to the lowest, at the first round the algorithm starts by computing the difference between the highest and the second-highest output. In general at round i the difference computed is
δ_i = oo₁ − oo_i + 1
. Then δ_i is subtracted from all oos, but the i + 1-th one.

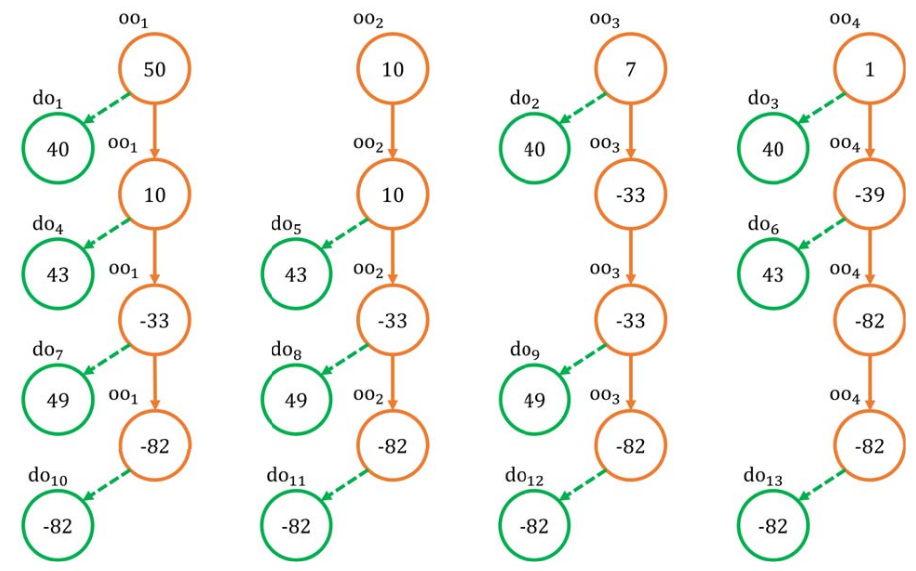
With reference to the figure above:

1. at the first round i = 1 output oo₁ = 50 is used decomposed into 40 = 50 − 10 = oo₁ − oo₂ and 10. then 40 is subtracted from all other inputs beside 00₂ = 10.
2. at the second round, the new original outputs are 10, 10,  − 33,  − 39 (yes, some are negative, it will be dealt with later on). Now oo₁ − oo₃ = 10 − ( − 33) = 43 and so 43 is subtracted from all oos beside oo₃
3. the new output at round i = 3 are …

You may see that from 4 oos in the example, we have 13 derived outputs do at the end. I t is easy to see that this maximizes the number of possible mappings.

There is one problem: how to deal with negative amounts? Here the solution is to introduce compensatory outputs: a third party service (or a pool) participates to the transaction and the decomposition to help achieving privacy in exchange of a fee. Using the compensatory outputs co the situation is like the figure below:

Discussion

• We can only talk about [Ni22] and [Mau17], since the other paper does not analyze the problem in sufficient details. Also, we analyze them from the point of view of a possible implementation in the decentralized mixer DMix.
• On the one hand [Ni22] seems to achieve a higher number of possible IOmappings, but at a heavy cost: the introduction of compensatory outputs which implies the need of pools and/or centralized services to help in the mixing. This is not that different from the use of coordinators in other mixing services such as Wasabi, after all.
• On the other hand the system presented in [Mau17] produces a lower number of possible IOmappings, but can be performed by participants alone with no external help.
• Furthermore, the work of [Mau17] gives no assurance of the fact that the number of derived outputs is minimal relative to the possible IOmappings. On the other hand the work of [Ni22] gives you and assurance of this. less outputs means less fees. so there is actually an incentive to minimize the number of outputs while preserving and maximizing the number of possible IOmappings.
• Both systems are deterministic: starting from the same outputs, every user would come to the same conclusions. This is very important in a decentralized setting, since no communication is needed by the parties once they know the original outputs of the other parties. On the other hand it is not possible to know the complete list of the derived outputs before knowledge of all output (or input, since in our use case they are the same) amounts. This implicitly means that no address exchange can be performed before knowing all the inputs and original outputs.

---

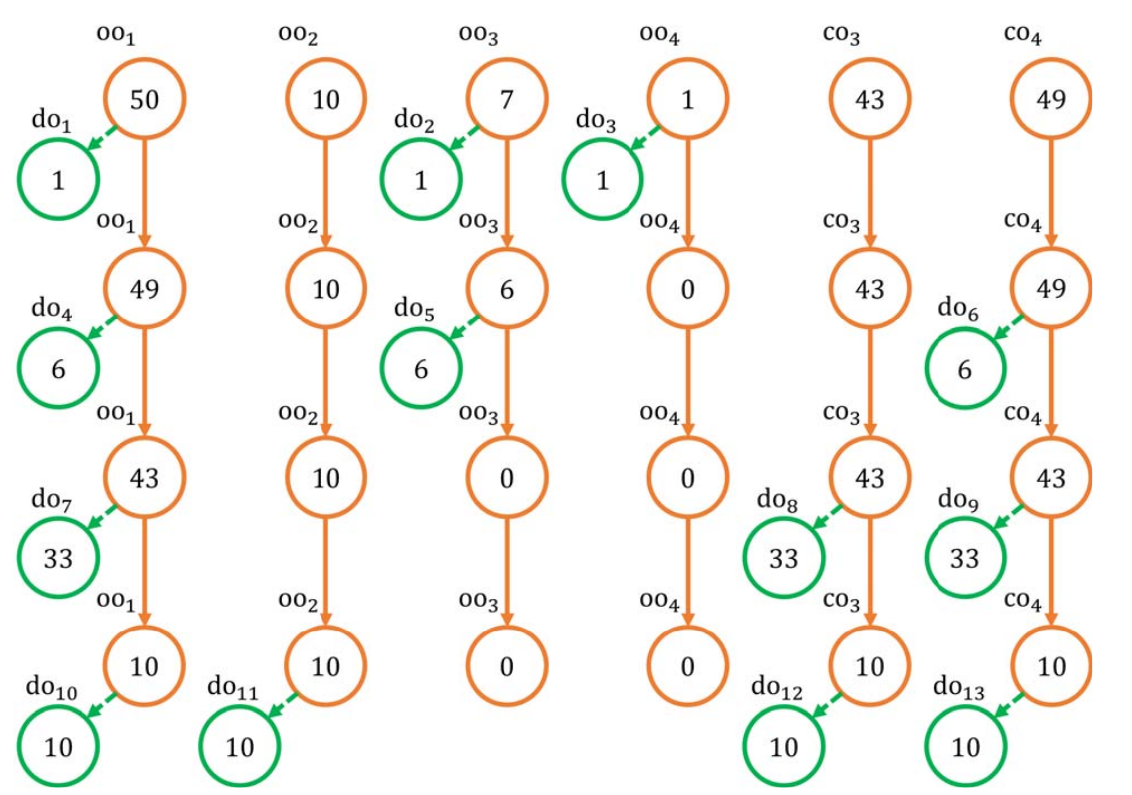
1. That’s because if the second output is the payment, then there is no reason to use more than one input, since any of the inputs alone would pay for it.↩︎

2. I may very well be wrong here! I you know about some other paper on the topi I would be very glad to edit the post and include it. you may write to me at @fadibarbara on Telegram or an email at me [at] fadibarbara.it .↩︎

---

I hope you liked this post. If you have comments, the best way to express them is by going on Telegram and comment on the dedicated post on the group.

Alternatively you can write me in private on Telegram or an email at me at fadibarbara .it .